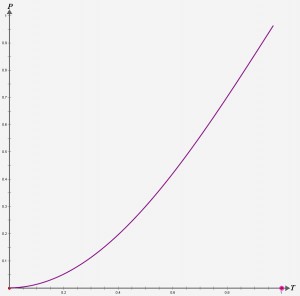
在mx.effects.easing包中,正弦缓动命名为Sine.as。正弦缓动所依据的方程为:
p(t) = sin(t * π / 2)
正弦和余弦都能够生成周期震荡的波形,而且它们只需要沿时间轴平移1/4个周期即π / 2,就可以互相转换。
正弦缓动的运动比二次缓动还要平缓,如下图所示。曲线并不十分弯曲,而且大部分都近似于45度的直线。
正弦缓动的缓入、缓出和缓入-缓出函数如下:
public static function easeIn(t:Number, b:Number, c:Number, d:Number):Number{
return -c * Math.cos(t / d * (Math.PI / 2)) + c + b;
}
public static function easeOut(t:Number, b:Number, c:Number, d:Number):Number{
return c * Math.sin(t / d * (Math.PI / 2)) + b;
}
public static function easeInOut(t:Number, b:Number, c:Number, d:Number):Number{
return -c / 2 * (Math.cos(Math.PI * t / d) - 1) + b;
}
缓入方程-c * Math.cos(t / d * (Math.PI / 2)) + c + b
= c * (1 – Math.cos(t / d * (Math.PI / 2))) + b
t / d的取值区间为[0,1],表达式Math.cos(t / d * (Math.PI / 2))的区间为[1,0],通过用1减去该表达式从而完成正弦缓入曲线。
缓出方程c * Math.sin(t / d * (Math.PI / 2)) + b,就是0到π / 2的正弦曲线。
缓入缓出方程 -c / 2 * (Math.cos(Math.PI * t / d) – 1) + b,整理为c / 2 * (-Math.cos(Math.PI * t / d) + 1) + b。即将标准余弦曲线沿水平时间轴垂直翻转并向上平移1个单位,取0至π之间的值。