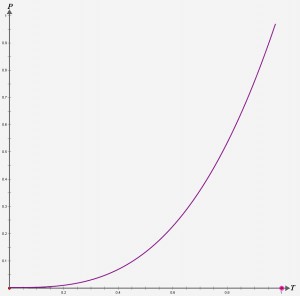
在mx.effects.easing包中,三次缓动命名为Cubic.as。三次缓动方程基于变量t的三次方:
p(t) = t3
大家知道,三次函数在定义域上单调递增,函数为奇函数,函数图像关于原点对称。三次缓动曲线比二次曲线增加速度更快,也就更为弯曲,如下图所示。
三次缓动的缓入、缓出和缓入-缓出函数如下:
public static function easeIn(t:Number, b:Number, c:Number, d:Number):Number{
return c * (t /= d) * t * t + b;
}
public static function easeOut(t:Number, b:Number, c:Number, d:Number):Number{
return c * ((t = t / d - 1) * t * t + 1) + b;
}
public static function easeInOut(t:Number, b:Number, c:Number, d:Number):Number{
if ((t /= d / 2) < 1) return c / 2 * t * t * t + b;
return c / 2 * ((t -= 2) * t * t + 2) + b;
}
三次缓入方程c * (t /= d) * t * t + b,从表达式上实际等价于c * t3 + b,只不过将参数t的值经过了标准化处理后,又重新赋给了t。从而也间接地改变了后面两个t的值。
三次缓出方程c * ((t = t / d – 1) * t * t + 1) + b,整理后实际为c * ((t – 1)3 + 1) + b。也就是将三次曲线向右、向上平移1个单位。结合三次函数的标准图像大家会看的非常清楚。
三次函数的缓入-缓出方程同样也是分为两个部分。当0 <= t < 1时,执行代码c / 2 * t * t * t + b,也就是c / 2 * t3 + b。和二次缓入-缓出方程一样,缓入只占到整个补间的位置改变的一半,所以c必须除以2。当1 <= t <= 2时,执行代码c / 2 * ((t -= 2) * t * t + 2) + b,整理一下就是c / 2 * ((t – 2)3 + 2) + b,将三次函数的图像向右、向上平移2个单位。