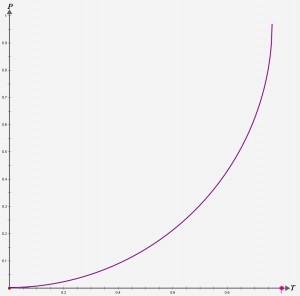
在mx.effects.easing包中，圆形缓动文件名为Circular.as。圆形缓动所依据的方程为：
这个方程根据半圆方程得到的，其中使用了平方根的计算。大家知道，圆的标准方程为(x – a)2 + (y – b)2 = r，其中(a, b)表示圆心，r表示半径。圆形缓动的方程展开后为：
t2 + (p – 1)2 = 1
也就表示以(0, 1)为圆心，半径为1的圆。其中定义域为[-1, 1]，值域为(-∞, 1]。图形下图所示。
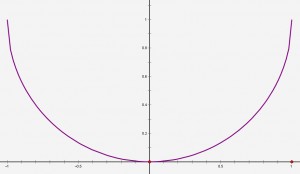半圆方程曲线
下图圆形缓动就是一段1/4圆的圆弧。它所生成的运动有着独特的风格，与五次缓动和指数缓动比较，圆形缓动的加速度更为突然。
圆形缓动曲线
圆形缓动的缓入、缓出和缓入-缓出函数如下：
public static function easeIn(t:Number, b:Number, c:Number, d:Number):Number{
return -c * (Math.sqrt(1 - (t /= d) * t) - 1) + b;
}
public static function easeOut(t:Number, b:Number, c:Number, d:Number):Number{
return c * Math.sqrt(1 - (t = t/d - 1) * t) + b;
}
public static function easeInOut(t:Number, b:Number, c:Number, d:Number):Number{
if ((t /= d / 2) < 1) return -c / 2 * (Math.sqrt(1 - t * t) - 1) + b;
return c / 2 * (Math.sqrt(1 - (t -= 2) * t) + 1) + b;
}
缓入方程-c * (Math.sqrt(1 – (t /= d) * t) – 1) + b，整理后就是c * (1 – Math.sqrt(1 – (t /= d) * t) + b，用数学方式表示就是 。由于自变量t的定义域为[0, 1]，所以该图形为图6-13中第一象限的1/4圆。
缓出方程c * Math.sqrt(1 – (t = t/d – 1) * t) + b，就是以(1, 0)为圆心，半径为1的圆。但自变量t的定义域为[0, 1]，因变量p >= 0。所以图形只取圆心左上的1/4圆弧。
缓入-缓出方程执行if ((t /= d / 2) < 1)后，使t值限定在0 <= t <= 2的范围，当0 <= t < 1时，执行-c / 2 * (Math.sqrt(1 – t * t) – 1) + b，可以看出就是半圆方程，且0 <= t < 1，所以图形为第一象限的1/4圆。当1 <= t <= 2时，执行c / 2 * (Math.sqrt(1 – (t -= 2) * t) + 1) + b。它代表的圆方程为(t – 2)2 + (p – 1)2 = 1。即以(2, 1)为圆形，半径为1的圆。且方程的定义域为[1, 2]，值域为[1, +∞]。所以方程应该表示以(2, 1)为圆形，以1为半径的圆的左上1/4圆弧。最后当然还是乘以位置的改变的一半即c / 2，以放大到所需的输出。最后加上初始偏移量b完成计算，并返回结果
缓入-缓出方程中的缓出曲线
