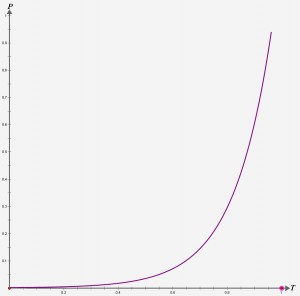
在mx.effects.easing包中，指数缓动命名为Exponential.as。指数缓动所依据的方程为：
p(t) = 2^10(t-1)
大家知道，指数函数y = ax的定义域为(-∞, +∞)，值域为(0, +∞)，都通过(0,1)点，当a > 1时，函数单调增加，当0 < a < 1时，函数单调递减。但标准指数桉树并不适用，这是由于缓动在t =0时位置不变，即为初始位置b，那就要求方程的结果为0，但指数函数无法为0。指数缓动所依据的方程是以2为底，指数为时间t减1并乘以10。这样就使t = 0，代入方程即为2-10约为0.0009765625，这样就能够获得一个足够小的位置。
如下图所示，指数缓动具有较大的弯曲幅度。

指数缓动曲线

指数缓动的缓入、缓出和缓入-缓出函数如下：

public static function easeIn(t:Number, b:Number, c:Number, d:Number):Number{
	return t == 0 ? b : c * Math.pow(2, 10 * (t / d - 1)) + b;
}
public static function easeOut(t:Number, b:Number, c:Number, d:Number):Number{
	return t == d ? b + c : c * (-Math.pow(2, -10 * t / d) + 1) + b;
}
public static function easeInOut(t:Number, b:Number, c:Number, d:Number):Number{
	if (t == 0)		return b;
	if (t == d)		return b + c;
	if ((t /= d / 2) < 1)		return c / 2 * Math.pow(2, 10 * (t - 1)) + b;
	return c / 2 * (-Math.pow(2, -10 * --t) + 2) + b;
}

缓入方程首先判断t是否为0，如果为0则返回结果0，这样就避免了方程无法确切得到0值的问题。方程c * Math.pow(2, 10 * (t / d – 1)) + b，下面直接使用t代表标准化操作的t / d。方程实际为c * 2^10(t-1) + b，就是将c * 2^10t + b向右移动1个单位，定义域为[0,1]。
缓出方程c * (-Math.pow(2, -10 * t / d) + 1) + b，整理为c * (-2^{-10 * t} +1) + b，也就是将函数c * 2^10t + b沿水平时间轴翻转，沿垂直位置轴再次翻转，并向上移动1个单位。但经过两次翻转并向上平移1个单位后，当t / d = 1时，代入方程c * (-2^{-10 * t / d} +1) + b为c * (-2^-10 +1) + b，结果为0.9990234375 * c + b。为了解决无法确切得到1值的问题，首先判断t是否等于d，如果t等于d，也就是t / d等于1，则返回 c + b。
缓入-缓出方程首先判断t值，如果t = 0，则返回b；如果t = 1，则返回 b + c。执行if ((t /= d / 2) < 1)后，使t值限定在0 <= t <= 2的范围。依然将曲线按照t的取值范围划分为两段，当0 <= t < 1时，执行c / 2 * Math.pow(2, 10 * (t – 1)) + b，整理后为c / 2 * 2^10(t-1) + b，就是指数缓入曲线。当1 <= t <= 2时，执行c / 2 * (-Math.pow(2, -10 * –t) + 2) + b，整理后为c / 2 * (-2^-10(t-1) + 2) + b。就是在缓入方程c / 2 * 2^10(t-1) + b的基础上，c / 2 * (-2^10(t-1)) + b是将曲线沿水平时间轴翻转，c / 2 * (-2^-10(t-1) +) + b则是在垂直翻转的基础上以t = 1为轴水平翻转，c / 2 * (-2^-10(t-1) + 2) + b在两次翻转的基础上向上平移2个单位，从而得到后半段的缓出曲线。

转载请注明：陈童的博客 » 指数缓动