• 计算几何算法1. 三角形和多边形的面积（2D及3D）
• 计算几何算法2. 关于线和点到线的距离（二维和三维）
• 计算几何算法3. 包含于多边形内的点的快速绕数
• 计算几何算法4. 关于平面以及点到平面的距离
• 计算几何算法5. 直线、线段和平面相交（2D和3D）

关于平面
平面方程
计算参数坐标
点到平面的距离
实现
pbase_Plane()
参考文献

关于平面

尽管欧几里得在《几何原本I》里把平面定义为除了点和线之外的第三个基本几何体，但是他没有证明任何关于平面的性质，这种情形延续到很久后的《几何原本XI》。即使在证明《几何原本XI》中定理的时候，他也没有使用在《几何原本I》中给出的关于平面的定义。到了现代，[Coxter, 1989a]给出了一个更精确的平面的定义：

定义：如果A,B,C三点不共线，则与三角形ABC任意一边或两边上任意两点所共线的所有点组成平面ABC。但是，欧几里得的定理XI.2和定理XI.13表明了希腊人知道一个平面可以由以下信息确定：

1. 由不共线的三点，
2. 由两条交叉直线，
3. 由一条直线和不在线上的一点，
4. 由一点和一条垂直线。

平面方程

所以，有许多方法来表示一个平面π。 有些在任意维度都可行，有些只在三维空间下可行。在任意维度下，总可以用三个非共线的点V₀=(x₀,y₀,z₀), V₁=(x₁,y₁,z₁), V₂=(x₂,y₂,z₂) 来作为最基本三角形的顶点。在三维空间下，这就可以使用下列方程来唯一确定一个平面的点(x,y,z)：

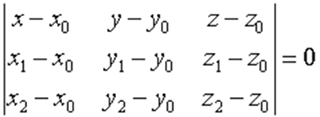
此外，在任意维度下，类似于参数线性方程，可以用方向向量u= V₁– V₀或v= V₂-V₀代替任意两个指定点V₁和V₂。 然后，已知一点V₀和不平行的方向向量u和v， 可得出平面PI的参数等式，即：

s和t是实数，即相对于原点V₀的坐标，u和v是基础向量。当0<=s, 0<=t, s+t<=1时P=V(s,t)在三角形T=V₀V₁V₂内。

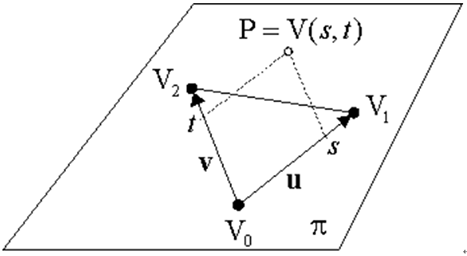
参数对(s,t)被称为相对于T的P=V(s,t)的参数坐标。当 s=0, t=0 或 s+t=1其中任意一个条件满足时，点P在T的一条边上。另外，T的三个顶点为V₀=V(0,0), V₁=V(1,0), V₂=V(0,1)。

一个类似的表述由对应于三角形T = V₀V₁V₂的P点的面积重心坐标给出。这种方法联系将中心点P和三角形(b₀,b₁,b₂)联系起来。使得：

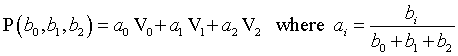
三角形(b₀,b₁,b₂)被称为P相对于三角形T的重心坐标，正交化的三角形(a₀,a₁,a₂)满足a₀ + a₁ + a₂ = 1，被称为P的面积（重心）坐标。显然，我们有P(a₀,a₁,a₂) = a₀V₀ + a₁V₁ + a₂V₂，因此任何总和为1的三角形(a₀,a₁,a₂)是一个有效的面积坐标。而且，面积坐标和平面上的所有的点有一一对应关系。这一点可以通过面积坐标和参数坐标的对应关系可以得出：a₀ = (1-s-t), a₁ = s, and a₂ = t.

相对于三角形T，面积坐标具有大量的有用性质。例如，仅仅当面积坐标全部非负时，P点位于三角形T的内部，就是a₀>=0, a₁>=0, and a₂>=0。

在3d中，对平面描述的另一个流行的且有用的表述是法线的形式，规定平面上的一个点V₀和一个垂直于它的向量n。这种表示由于它的紧凑和高效可用于计算交叉点。但是，它仅仅用于在3d空间中来定义平面。在更高的维度上，这种表示定义了一个n-1维线性子空间。

在三维中，平面的法向量n可以通过平面上三个点V₀V₁V₂的叉乘来计算，即n = u×v = (V₁-V₀)×(V₂-V₀)。那么，平面上的任意点都满足公式：

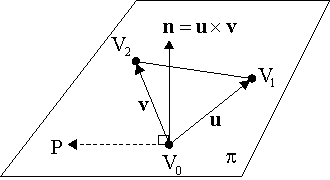对于 n = (a,b,c), P = (x,y,z)和 d =(n · V₀)，方程为：

注意，描述平面的线性方程的系数(a,b,c)给出了垂直于平面的向量。当d=0，π穿过原点。

经常使用单位向量来简化公式。通过分解n，用|n|=sqrt(a²+b²+c²)，这样可以说方程ax+by+cz+d=0被归一化了。而且，当|n|=1时，n的系数a,b,c是向量n在xyz坐标中的方向余弦。同时，当|n|=1是，d是原点到平面的垂直距离，这一点我们将在下一节说明。

我们能从一种表示方法向另一种表示方法转换。例如，给出一个平面的2条非平行向量，它们的叉乘得出法向量。相应地，给定一个法向量，可以找到两条独立的垂直于它的矢量。例如，给定n = (a,b,c)且a!=0，那么u=(-b,a,0) 和 v=(-c,0,a)都垂直于n，这是由于它们满足u · n = 0和v · n = 0。这样，平面上三个非共线点是V₀, V₀+u,和V₀+v。

计算参数坐标

然而，这样的转换涉及很多复杂的计算。也就是说，找到已知的三维空间中的点P=(x,y,z)相对于三角形T=V₀V₁V₂的参数或重心坐标需要复杂的计算。我们首先设定u=V₁-V₀, v=V₂-V₀, w=P-V₀，然后，我们计算P的参数坐标(s,t)从而得出w=su+tv。当P在平面T内时得到存在且唯一的解。最后，点P=b₀V₀+b₁V₁+b₂V₂的重心坐标等于：b₀=(1-s-t), b₁=s, b₂=t, 它满足b₀+b₁+b₂=1。

为了解这个方程，我们设定一个一般化的垂直点积。对于一个有法向量n的二维平面π，向量a位于平面内（即a满足n·a = 0），定义π的一般化的垂直运算符为：a^⊥= n × a。那么，a^⊥成为平面π内的另一个向量（由于n·a^⊥ = 0），而且它垂直于原来的向量a（由于a·a^⊥ = 0）。而且，这个新的垂直运算符是线性向量，即，(Aa+Bb)^⊥=Aa^⊥+Bb^⊥，这里a和b是向量而A和B是常量。注意到，如果π是二维xy平面(z=0)且有n=(0,0,1), 则它恰恰就是[Hill, 1994]给出的垂直运算符。

现在，求解方程：w = su + tv。首先，在等号两边同时点积v^⊥，得到w · v^⊥ = su · v^⊥ + tv · v^⊥= su · v^⊥然后求s的解。类似的， 在等号两边同时点积u^⊥，这将得到w · u^⊥= su · u^⊥+ tv · u = tv · u^⊥然后求t的解。我们得到：

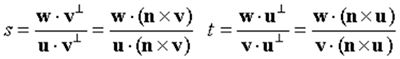
只要三角形T是非退化的（即有非零的面积）那么分母一定非零。当T退化成一个线段或一个点，它在任何情况下都不能唯一确定一个平面了。

虽然我们使用了3次叉乘，但对于任何三个向量a b c，有：(a × b) × c = (a · c) b – (b · c) a。简化如下：

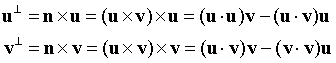
我们现在用点积公式可以计算s和t：

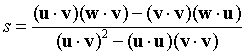
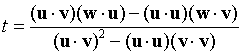
其中有5个独立的的点积运算。我们整理方程，发现2个分母是相同的，所以仅需要计算一次。

点到平面的距离

任意3d点P₀ = (x₀,y₀,z₀)到平面π：ax+by+cz+d=0的距离，可以通过点积得到向量(P₀-V₀)在n上的映射。如图所示：

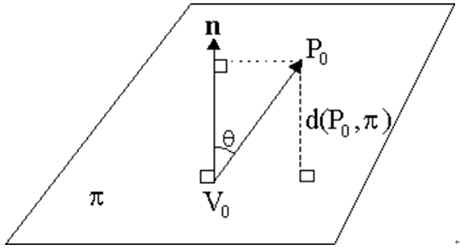
公式为：

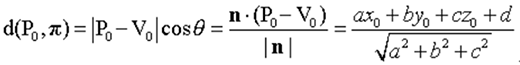
对于单位法向量，即当|n|=1时，这个等式可简化为：

表示了d是从原点(0,0,0)到平面π的距离。

这个公式给出了一个有符号的距离，在平面的一边为正在另一边则为负。所以这个距离的绝对值即是绝对距离。否则，在法向量一边的点，距离为正。由于这个性质，d(P₀,π)的正负可用来测试已知点在平面的哪一侧。例如，如果P₀P₁为一条线段，它只有在平面的两侧才能和平面π相交，即d(P₀,π) d(P₁,π) < 0；相反，d(P₀,π) d(P₁,π) > 0时不相交。如果d(P₀,π) d(P₁,π) = 0，则意味着两个端点其中之一或者全部在平面π内。当两个端点都在平面π内时，则线段P₀P₁位于平面内。

这个公式和2d空间中一个点到一条线的距离公式非常类似。另外请注意，我们并没有计算从点到平面的垂直相交点。

然而，在有些情况下想知道点P₀到平面π的正交投影。它可以通过做一条经过点P₀垂直于平面π的直线，计算和平面π的交点。经过P₀的垂直线由以下公式给出：P(s) = P₀ + sn。当 P(s)满足平面方程：n · (P(s)-V₀) = 0时和平面π相交。解此方程得到相交点S_π，我们得到：

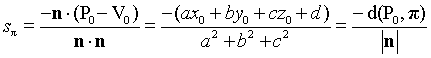
交点为：

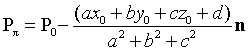
对于特殊情况，当P₀ = (0,0,0)，则有：P_π = –dn / |n|²，作为原点到平面的正交投影。我们看到：d(0,π) = d(0,P_π) = d / |n|。当n是单位法向量时，d(0,π) = d。

实现：

// Copyright 2001, softSurfer (www.softsurfer.com)
// This code may be freely used and modified for any purpose
// providing that this copyright notice is included with it.
// SoftSurfer makes no warranty for this code, and cannot be held
// liable for any real or imagined damage resulting from its use.
// Users of this code must verify correctness for their application.
// Assume that classes are already given for the objects:
//    Point and Vector with
//        coordinates {float x, y, z;}
//        operators for:
//            Point  = Point ± Vector
//            Vector = Point - Point
//            Vector = Scalar * Vector    (scalar product)
//    Plane with a point and a normal {Point V0; Vector n;}
//===================================================================
// dot product (3D) which allows vector operations in arguments
#define dot(u,v)   ((u).x * (v).x + (u).y * (v).y + (u).z * (v).z)
#define norm(v)    sqrt(dot(v,v))  // norm = length of vector
#define d(u,v)     norm(u-v)       // distance = norm of difference
// pbase_Plane(): get base of perpendicular from point to a plane
//    Input:  P = a 3D point
//            PL = a plane with point V0 and normal n
//    Output: *B = base point on PL of perpendicular from P
//    Return: the distance from P to the plane PL
float pbase_Plane( Point P, Plane PL, Point* B)
{
    float    sb, sn, sd;

    sn = -dot( PL.n, (P - PL.V0));
    sd = dot(PL.n, PL.n);
    sb = sn / sd;

    *B = P + sb * PL.n;
    return d(P, *B);
}
//===================================================================

参考文献：

Donald Coxeter, Introduction to Geometry (2nd Edition), Sect 12.4 “Planes and Hyperplanes”, John Wiley & Sons (1989a)
Donald Coxeter, Introduction to Geometry (2nd Edition), Sect 13.7 “Barycentric Coordinates”, John Wiley & Sons (1989b)
Euclid, The Elements, Alexandria (300 BC)
Andrew Hanson, “Geometry for N-Dimensional Graphics”  in Graphics Gems IV (1994)
Thomas Heath, The Thirteen Books of Euclid’s Elements, Vol 1 (Books I and II) (1956)
Thomas Heath, The Thirteen Books of Euclid’s Elements, Vol 3 (Books X-XIII) (1956)
Francis Hill, “The Pleasures of ‘Perp Dot’ Products” in Graphics Gems IV (1994)

转载请注明：陈童的博客 » 计算几何算法4. 关于平面以及点到平面的距离