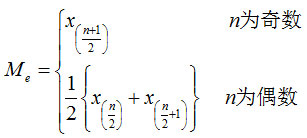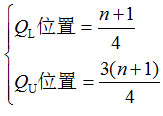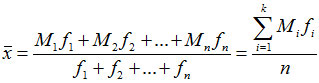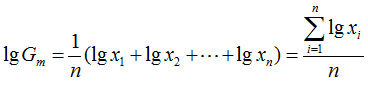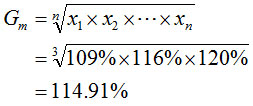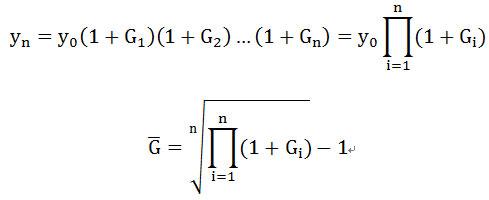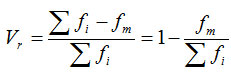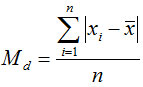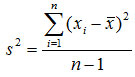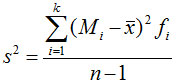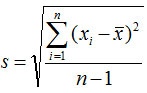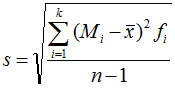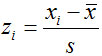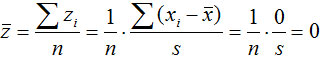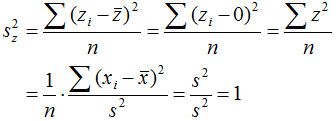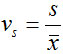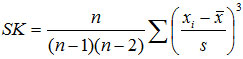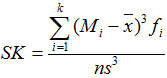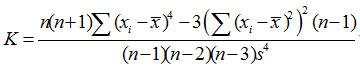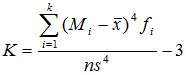三、数据的概括性度量
数据分布的特征可以从三个方面进行描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布偏斜程度和峰度。
1. 集中趋势的度量
集中趋势(Central tendency)是指一组数据向某一中心值靠拢的倾向,它反映了一组数据中心点的位置。
1.1 分类数据:众数
众数(Mode):一组数据中出现频数最多的变量值,用Mo表示。一般适合于数据量较多时使用,且不受极端值的影响;一组数据可能没有众数或有几个众数。
| 无众数 | 一个众数 | 多于一个众数 |
 |
 |
 |
例:
| 不同品牌饮料的频数分布 | |||
| 饮料品牌 | 频数 | 比例 | 百分比(%) |
| 可口可乐旭日升冰茶
百事可乐 汇源果汁 露露 |
1511
9 6 9 |
0.300.22
0.18 0.12 0.18 |
3022
18 12 18 |
| 合计 | 50 | 1 | 100 |
解:这里的变量为“饮料品牌”,这是个分类变量,不同类型的饮料就是变量值。所调查的50人中,购买可口可乐的人数最多,为15人,占被调查总人数的30%,因此众数为“可口可乐”这一品牌,即Mo=可口可乐
1.2 顺序数据:中位数和分位数
中位数(Median):一组数据排序后处于中间位置上的变量值,用Me表示。
中位数位置的确定:
四分位数:一组数据排序后处于25%和75%位置上的值。
四分位数位置的确定:
1.3 数值型数据:平均数
平均数(Mean):一组数据相加后除以数据的个数而得到的结果。
(1)简单平均数和加权平均数
根据未经分组整理的原始数据计算平均数。设一组样本数据为x1,x2,…,xn,样本容量为n,则样本平均数用![]() 表示,计算公式为:
表示,计算公式为: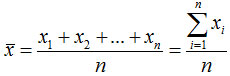
根据分组数据计算平均数。设原始数据被分成k组,各组的组中值分别用M1,M2,…Mn表示,各组变量出现的频数分别用f1,f2,…fn表示,则平均数的计算公式为:
(2)几何平均数
几何平均数(geometric mean):n个变量值乘积的n次方根,用Gm表示
几何平均数的计算公式为:
它可以看作是平均数的一种变形:
例:某水泥生产企业1999年的水泥产量为100万吨,2000年与1999年相比增长率为9%,2001年与2000年相比增长率为16%,2002年与2001年相比增长率为20%。求各年的年平均增长率。
年平均增长率=114.91%-1=14.91%
设开始的数值为y0,逐年增长率为G1,G2,…Gn,第n年的数值为:
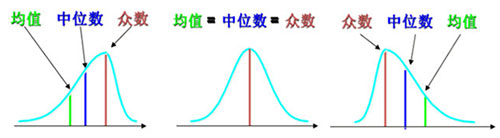
1.3 众数、中位数和平均数的比较
众数的特点:(1)不受极端值影响;(2)具有不惟一性;(3)数据分布偏斜程度较大且有明显峰值时应用
中位数的特点:(1)不受极端值影响;(2)数据分布偏斜程度较大时应用
平均数的特点:(1)易受极端值影响;(2)数学性质优良;(3)数据对称分布或接近对称分布时应用
2. 离散程度的度量
数据的分散程度是数据分布的另一个重要特征,它所反映的是各变量值远离其中心值的程度,因此也称为离中趋势。
2.1 分类数据:异众比率
异众比率(variation ratio):非众数组的频数占总频数的比率,用Vt表示。用异众比率主要用于衡量众数对一组数据的代表程度。异众比率的计算公式为:
异众比率越大,说明非众数组的频数占总频数的比重越大,众数的代表性就越差;异众比率越小,说明非众数组的频数占总频数的比重越小,众数的代表性越好。
2.2 顺序数据:四分位差
四分位差(quartile deviation):也称为内距或四分间距,上四分位数与下四分位数之差,用Qd表示。
四分位差的计算公式为:Qd = QU – QL
四分位差反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中,数值越大,说明中间的数据越分散。它不受极端值的影响,一般用它来衡量中位数的代表性。
2.3 数值型数据:方差和标准差
(1)极差(Range):也称全距,一组数据的最大值与最小值之差,用R表示。
极差的计算公式为:R = max(xi) – min(xi)
(2)平均差(mean deviation):也称平均绝对离差,各变量值与其平均数离差绝对值的平均数,用Md表示。
未分组数据计算平均差的公式为:
分组数据平均差的公式为:
(3)方差和标准差
方差和标准差是数据离散程度的最常用测度值,它反映了各变量值与均值的平均差异。根据总体数据计算的,称为总体方差或标准差,记为s2(s);根据样本数据计算的,称为样本方差或标准差,记为s2(s)。
未分组数据:
分组数据:
标准差(standard deviation):方差的平方根
未分组数据:
分组数据:
2.4 相对位置的度量:标准分数
(1)标准分数
标准分数(standard score):也称为标准化值或z分数,变量值与其平均数的离差除以标准差后的值。
设标准分数为z,则有:
标准分数主要是对某一个值在一组数据中相对位置的度量,它可用于判断一组数据是否有离群点(outlier),也用于对变量的标准化处理。
标准分数具有平均数为0,标准差为1的特征:
(2)经验法则
经验法则表明:当一组数据对称分布时
- 约有68%的数据在平均数加减1个标准差的范围之内
- 约有95%的数据在平均数加减2个标准差的范围之内
- 约有99%的数据在平均数加减3个标准差的范围之内
(3)切比雪夫不等式
如果一组数据不是对称分布,经验法则就不再适用,这时可使用切比雪夫不等式,它对任何分布形状的数据都适用。切比雪夫不等式提供的是“下界”,也就是“所占比例至少是多少”。对于任意分布形态的数据,根据切比雪夫不等式,至少有1-1/k2的数据落在k个标准差之内。其中k是大于1的任意值,但不一定是整数
对于k=2,3,4,该不等式的含义是
- 至少有75%的数据落在平均数加减2个标准差的范围之内
- 至少有89%的数据落在平均数加减3个标准差的范围之内
- 至少有94%的数据落在平均数加减4个标准差的范围之内
2.5 相对离散程度:离散系数
离散系数(coefficient of variation):也称为变异系数,一组数据的标准差与其相应的平均数之比。
计算公式为:
离散系数的作用主要是用于比较不同样本数据的离散程度。离散系数大就说明数据的离散程度大,离散系数小就说明数据的离散程度小。
3. 偏态和峰态的度量
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还需要知道数据分布的形状是否对称、偏斜的程度以及分布的扁平程度等。偏态和峰态就是对分布形状的测度。
3.1 偏态及其测度
偏态(skewness):数据分布的不对称性。
偏态系数(SK):对数据分布不对称性的度量值。
偏态系数的计算方法有很多,对于未分组数据通常采用下面的公式:
对于分组数据,一般采用下面的公式:
3.2 峰态及其测度
峰态(kurtosis):数据分布的平峰或尖峰程度。
峰态系数(K):对数据分布峰态的度量值。
如果一组数据服从标准正态分布,则峰态系数等于0;如果峰态系数明显不同于0,表明分布比正态分布更平或更尖,通常称为平峰分布或尖峰分布。
未分组数据通常采用如下的公式:
分组数据采用如下的公式:
转载请注明:陈童的博客 » 集体智慧算法——统计学基础2