- 计算几何算法1. 三角形和多边形的面积(2D及3D)
- 计算几何算法2. 关于线和点到线的距离(二维和三维)
- 计算几何算法3. 包含于多边形内的点的快速绕数
- 计算几何算法4. 关于平面以及点到平面的距离
- 计算几何算法5. 直线、线段和平面相交(2D和3D)
交叉数
边缘交叉规则
伪码:CN Inclusion
绕数
伪码:WN Inclusion
改进
边界框或边界球
三维平面多边形
凸多边形与单调多边形
实现
cn_PnPoly()
<wn_PnPoly()
参考文献
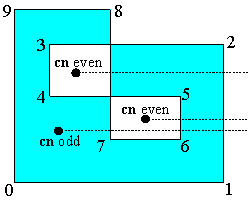
确定一个点是否包含在2D平面多边形中是一个产生了许多有趣算法的几何问题。两种常用的方法是:1.交叉数法记录从点P出发的射线越过多边形边界的次数。当交叉数为偶数时,这个点在外面;而当交叉数为奇数时,这个点在里面。这个方法有时候被称为“奇-偶”检测。2.绕数法记录多边形绕过该点的次数。只有当绕数等于0的时候这个点在外面; 除此之外点都在内部。如果一个多边形是简单的(即没有自我交叉),则对于所有的点这两种算法都得出同样的结果。但是对于一个非简单多边形,对于某些点来说利用这两种算法将得到不同的答案。例如,当一个多面性自我重叠,则处于重叠区域的点被交叉数法认为是在外部的,但是绕数法认为它在内部,如图所示:
| 交叉数法 | 绕数法 |
 |
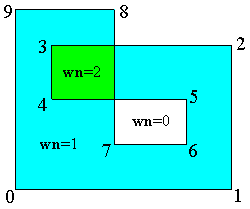 |
| 顶点计数:0 1 2 3 4 5 6 7 8 9 |
在这个例子中,重叠区域的点有 wn=2, 意味着它两次属于这个多边形。显然,绕数法给出了比交叉数法更直接的答案。尽管如此,经常使用的还是交叉数法用,这是因为人们认为cn比wn有更高的计算效率(20倍!) [O’Rourke,1998]。但是事实并非如此,通过计数标记的交叉点,wn 和cn具有相同的效率。事实上,我们的实现wn_PnPoly()函数比[Franklin, 2000],[ Haines, 1994]或[O’Rourke, 1998]的cn算法更快,尽管[Moller & Haines,1999] 的 cn“PointInPolygon()” 程序完全比的上我们的wn 算法。所以,出于正确并且有效的几何学因素, wn 算法是判定一个点是否包含在一个多边形中的首选算法。
交叉数
这种方法使用从点P出发的射线与多边形边缘交叉的次数来判定P在多边形内还是多边形外。如果这个次数是偶数则在多边形外;如果是奇数则在多边形内。这很容易直观的理解。每次射线穿过边界,则内-外奇偶校验改变(因为边界就是将里与外分开的,对吗?)。最后,任何一条射线都将越过多边形,处于多边形之外。所以,如果点在内部,这些表示穿越顺序的 –> 一定是: 内–>外–>… –>内–>外,它们是奇数。同样的,如果点在外部,有偶数个依照这种顺序的交叉:外–>…内–>外。
在实现 cn算法的过程中,必须确保只有交叉才改变内-外的奇偶检测。尤其是对于射线穿过顶点的特例必须正确的处理。它们包括以下几种交叉:
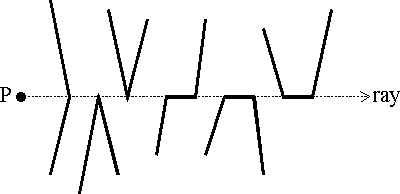
此外,必须判定在多边形边缘上的点属于内部还是外部。一种标准的做法是,在左侧或者下边的点属于内部,在右侧或者顶边的点在外部。这种方式决定了,如果两个截然不同的多边形公用一条边界线段,则这条公共线段上的点只能属于其中的某一个多边形,但是不能同时属于二者。这样就避免了一些可能出现的问题。一个简单的“交叉数”算法选择一条水平射线延伸至P的右侧并且平行于X轴正方向。 运用这条特殊的射线,可以容易的计算多边形边界与它的交叉点。它甚至更容易判断没有交叉点的情况。通过计算交叉点总数, cn算法只需要遍历多边形的所有边,测试每一个交叉点,一旦发生交叉则增加cn。此外,交叉点测试必须处理边缘上的特殊情况和问题。 这就是——
边缘交叉规则
1. 一个向上的边包括它的起始点,不包括它的终止点;2. 一个向下的边不包括它的起始点,包括它的终止点;3. 排除所有水平的边;4. 边-射线的交叉点集必须严格的出现在P的右侧。这些规则可以应用到前面的特殊例子中,并且可以看到他们正确的确定了有效的交叉点。第四条规则的原理是点在右侧边缘属于外部,左侧边界属于内部。
伪代码: Crossing # Inclusion
这个算法非常有名,很容易能够表达边界交叉的规则。一个多边形将被表示为顶点数是 V[n+1]的数组且V[n]=V[0],流行的实现逻辑如下:
typedef struct {int x, y;} Point;
cn_PnPoly( Point P, Point V[], int n )
{
int cn = 0; // 记录交叉点数
// 遍历多边形的所有边
for (each edge E[i]:V[i]V[i+1] of the polygon) {
if (E[i] crosses upward ala Rule #1
|| E[i] crosses downward ala Rule #2) {
if (P.x < x_intersect of E[i] with y=P.y) // 规则 #4
++cn; // P.x右侧的有效交叉点
}
}
return (cn&1); // 0 如果是奇数(out),1 如果是偶数 (in)
}
请注意,向上和向下交叉检测满足规则 #1 和 #2 同时排除水平边缘(规则#3)。重要的是,只要几个测试就可以完成大量工作使之成为一个优雅的算法。但是,交叉数方法的有效性基于“Jordan 曲线定理”,该定理强调一个简单的封闭曲线正好分为两个连通的二维平面:一个有界限的“内部”与一个无边界的“外部”。要注意的是曲线必须是简单的(无自交点),否则它可能有多于两个的组成部分,这样边缘交叉点改变奇偶的检测就将无法保证。对于一个封闭曲线,还有一个无界的“外部”部分;但有界的组件可以是内部或外部。他们可以是两个有边界的内部组件并且共享一条边,当穿过它们的公共边是将不改变奇偶检测。
绕数
另一方面,绕数可以准确的确定一个点是否在一个非简单封闭多边形中。它依靠记录多边形绕过该点的次数来实现。当多边形根本不围绕该点旋转时,这个点在外部,此时绕数 wn= 0。更通俗的说,对于任意一个在二维平面的连续封闭曲线可以确定关于某点的绕数 wn。使C(u)=(x(u),y(u)), 当0<=u<=1有C(0)=C(1),是一个连续的二维曲线,使 P成为一个不在C(u)中的点。然后,确定从 P 到 C(u)的向量CP(u)=C(u)-P,并使它的单位方向矢量——从曲线C到单位圆S1的映射为 W(u)=CP(u)/|CP(u)| ,因此它可以在坐标上表示为 W(u)=(cos (u), sin(u)) 当 (u) 是一个逆时针方向角。绕数 wn 则等于整数次 W(u) 环绕 S1。这相当于 S1的同伦类,并且可以通过积分计算:
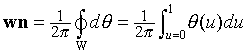
当曲线 C是一个有顶点 V0,V1,…,Vn=V0的多边形时,这个积分减少了角度的总和。所以,若θi=angle(PVi,PVi+1)则可以得到:
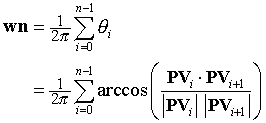 |
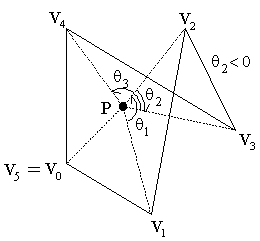 |
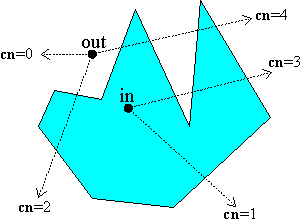
这个公式显然不是很有效率,因为它使用一个昂贵的arccos()三角函数。但是,一个简单的观察让我们找到更有效率的替代公式。选择 S1上的一个点 Q。然后曲线 W(u) 环绕S1,它传递给 Q一定的次数。当它逆时针经过Q我们的计数增加(+1),当它顺时针经过Q时计数减少(-1),然后累加的总和就是W 环绕 S1的总数。并且它等同于绕数 wn。此外,如果我们采用一个起始于 P的射线R向矢量Q的方向延伸,那么射线R和曲线C的相交点和W穿过Q的点对应。但我们必须区分正向与负向的交叉点即 C 穿越 R时是“从右到左”还是“从左到右”。这可以通过曲线C的法向量与方向向量Q之间的点积符号来判断,当曲线 C 是一个多边形,每一条边只需要做一次这样的判断。作为一条从P出发的水平射线R ,测试边的端点是不是在射线的范围内。如果边缘从下到上的穿过正向射线,则交叉值为正 (+1);但是如果它从上到下的穿过,则交叉值为负 (-1)。将所有交叉值相加得到 wn。例如:
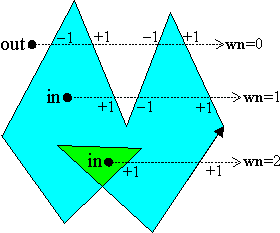
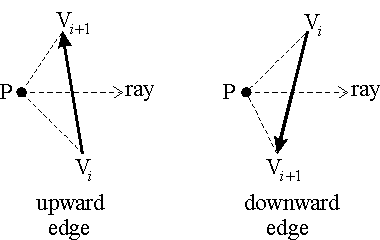
此外,使用 isLeft()函数可以避免计算实际的交点;但是对于上升边和下降边有不同的使用方法。如果向上的边缘穿过射线到了 P的右方,则 P在边的左侧,因为三角形ViVi+1P 以逆时针为方向。另一方面,下降边穿过射线将获得一个在右侧的P,因为三角形ViVi+1P 将以顺时针为方向。
伪代码: Winding # Inclusion
生成的 wn 算法如下, 它适应 cn 算法并且使用前面提到特例中的相同的边界交叉规则。
typedef struct {int x, y;} Point;
wn_PnPoly( Point P, Point V[], int n )
{
int wn = 0; // 绕数计数
// 遍历所有的边
for (each edge E[i]:V[i]V[i+1] of the polygon) {
if (E[i] crosses upward ala Rule #1) {
if (P is strictly left of E[i]) // 规则 #4
++wn; // 上行在P.x右侧的交叉点
}
else
if (E[i] crosses downward ala Rule #2) {
if (P is strictly right of E[i]) // Rule #4
--wn; // 下行在P.x右侧的交叉点
}
}
return wn; // =0 <=> P 在 V[] 之外
}
显然,绕数算法与交叉数算法具有类似的效率。尽管如此,由于它更准确, 绕数算法应是确定一个任意点是否被包含在多边形中的首选方法。wn 算法的效率可以通过重新安排交叉测试对得到进一步的提高。它将在下面展示的 wn_PnPoly()的具体实现中有所体现。在这个程序中,所有的边界完全在P之上或之下,在两个不等式测试后就被排除。然而,目前流行的cn 算法的实现对于每条被否定的边至少使用了三次不等式测试。在实际应用中,由于在一个非常大的多边形中可以排除大多数的边,大约减少了33% (或者更多的) 比较次数。在测试运行时使用非常大(1,000,000条边)随机多边形(边长<多边形直径的1 / 10) 和1000随机测试点(在多边形的边界框内),效率提高了20%左右。
改进
软件开发人员还应该知道有一些点在多边形中的算法的改进。我们仅举几个属于射线交叉算法的例子。 但是,也有在特殊情况下表现更好的其他技术,诸如检查包含在小的凸多边形中例如三角形的情况。
边界框或球
在交叉测试中在测试所有的边之前,首先测试一点是否位于多边形的边界框或者边界球内是很有效的做法。如果这个点在边界框或者边界球外,那也就是毫无疑问地在多边形之外,不需要其它的检测了。但是,我们必须预先计算出来边界框(顶点的最大最小x、y坐标)或者边界球(圆心与最小半径),并存储起来以便将来使用。一般情况下,如果有很多个点需要检测这样做是非常值得的。
三维平面多边形
在3D应用中,人们有时想要测试一个点或一个多边形是否在同一平面中。 例如,多面体的面所在的平面可能与射线有一个交点,想要检测它是否在多面体面的内部。3D 包含测试可以通过将点和多边形投影到2D而解决问题。要做到这一点,我们通常只是简单地忽略一个三维坐标中的一个而使用另外的两个。为了选择最佳的坐标,计算平面的法向量,并且选择一个具有最大绝对值的坐标。这样将给出多边形的最大投影面积,增强计算的鲁棒性。
凸多边形与单调多边形
当已知多边形为凸多边形时,可以加快一些计算。例如,可以花费O(log n)时间来计算边界框,而不是非凸多边形的O(n)时间。同样的,点包含测试可以使用 O(log n)时长。更普遍的,下面的算法用来计算凸多边形和单调多边形。一个凸多边形或者y型单调多边形,可以把它分成两条折线,一条沿y轴增加,一条沿y轴减少。在最大y与最小y处分裂。请注意,这些顶点在多边形边界框的顶部和底部,如果他们都高于或低于射线,那么测试点在多边形外。另外,每条折线与射线相交一次,这样在每条折线的顶点上通过折半查找就可以找到所有的交叉边。结果只需 O(log n) (预处理和运行) 进行计算。在下面的例子中,仅仅需要3次折半查找(A1, A2, A3向上的,B1, B2, B3 向下的):

这种方法也是适用于在任意方向单调的多边形。后来有人用了一条从P出发的垂直于单调方向的射线, 并且算法很容易改写。
实现
这是一个关于多边形中点的包含问题的绕数算法的”C++”实现。我们只给出二维的例子,使用最简单的点和多边形结构,或许和您的应用不同。
// Copyright 2001, softSurfer (www.softsurfer.com)
// This code may be freely used and modified for any purpose
// providing that this copyright notice is included with it.
// SoftSurfer makes no warranty for this code, and cannot be held
// liable for any real or imagined damage resulting from its use.
// Users of this code must verify correctness for their application.
// a Point is defined by its coordinates {int x, y;}
//===================================================================
// isLeft(): tests if a point is Left|On|Right of an infinite line.
// Input: three points P0, P1, and P2
// Return: >0 for P2 left of the line through P0 and P1
// =0 for P2 on the line
// // See: the January 2001 Algorithm "Area of 2D and 3D Triangles and Polygons"
inline int
isLeft( Point P0, Point P1, Point P2 )
{
return ( (P1.x - P0.x) * (P2.y - P0.y)
- (P2.x - P0.x) * (P1.y - P0.y) );
}
//===================================================================
// cn_PnPoly(): crossing number test for a point in a polygon
// Input: P = a point,
// V[] = vertex points of a polygon V[n+1] with V[n]=V[0]
// Return: 0 = outside, 1 = inside
// This code is patterned after [Franklin, 2000]
int
cn_PnPoly( Point P, Point* V, int n )
{
int cn = 0; // the crossing number counter
// loop through all edges of the polygon
for (int i=0; i<n; i++) { // edge from V[i] to V[i+1]
if (((V[i].y <= P.y) && (V[i+1].y > P.y)) // an upward crossing
|| ((V[i].y > P.y) && (V[i+1].y <= P.y))) { // a downward crossing
// compute the actual edge-ray intersect x-coordinate
float vt = (float)(P.y - V[i].y) / (V[i+1].y - V[i].y);
if (P.x < V[i].x + vt * (V[i+1].x - V[i].x)) // P.x < intersect
++cn; // a valid crossing of y=P.y right of P.x
}
}
return (cn&1); // 0 if even (out), and 1 if odd (in)
}
//===================================================================
// wn_PnPoly(): winding number test for a point in a polygon
// Input: P = a point,
// V[] = vertex points of a polygon V[n+1] with V[n]=V[0]
// Return: wn = the winding number (=0 only if P is outside V[])
int
wn_PnPoly( Point P, Point* V, int n )
{
int wn = 0; // the winding number counter
// loop through all edges of the polygon
for (int i=0; i<n; i++) { // edge from V[i] to V[i+1]
if (V[i].y <= P.y) { // start y <= P.y if (V[i+1].y > P.y) // an upward crossing
if (isLeft( V[i], V[i+1], P) > 0) // P left of edge
++wn; // have a valid up intersect
}
else { // start y > P.y (no test needed)
if (V[i+1].y <= P.y) // a downward crossing
if (isLeft( V[i], V[i+1], P) < 0) // P right of edge
--wn; // have a valid down intersect
}
}
return wn;
}
//===================================================================
参考文献
James Foley, Andries van Dam, Steven Feiner & John Hughes, Computer Graphics (2nd Edition in C), Section 19.2.8 “Filled Primitives” (1996)
Wm. Randolph Franklin, “PNPOLY – Point Inclusion in Polygon Test” Web Page (2000)
Eric Haines, “Point in Polygon Strategies” in Graphics Gems IV (1994)
[Note: an early draft of this paper is online at: http://www.acm.org/pubs/tog/editors/erich/ptinpoly/]
Tomas Moller & Eric Haines, Real-Time Rendering, Section 10.6 “Ray/Polygon Intersection” (1999)
Joseph O’Rourke, Computational Geometry in C (2nd Edition), Section 7.4 “Point in Polygon” (1998)
Joseph O’Rourke (ed.), Graphics Algorithms FAQ, § 2.03: “How do I find if a point lies within a polygon?” (2001)
John M. Snyder & Alan H. Barr, “Ray Tracing Complex Models Containing Surface Tessellations”, Computer Graphics 21(4), 119-126 (1987) [also in the Proceedings of SIGGRAPH 1987]
转载请注明:陈童的博客 » 计算几何算法3. 包含于多边形内的点的快速绕数



