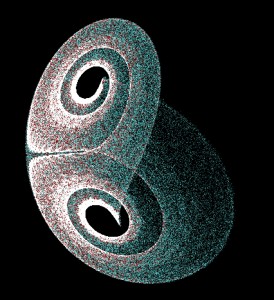
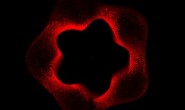
本博客中关于Flash平台三维粒子的示例,以前都利用了pv3d引擎。不通过三维引擎,直接利用Flash Player 10的API能达到什么样的效果呢,下面就让我们通过构造粒子形状、粒子灯光和粒子图片运动来展示下。
Edward Lorenz通过美丽而简单的方程向我们论证了动态系统的混沌行为,由于Lorenz的发现,这个方程在混沌历史十分有名。它有4个参数,a,b,c和dt,方程为:
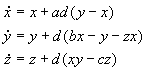
利用链表、Vector等优化技术构造30万个粒子来构造Lorenz attractor,方程使用ActionScript表示为:
参数:a,b,c,d
公式: finalX = x+ad(y-x)
finalY = y+d(bx-y-zx)
finalZ = z+d(xy-cz)
package{
import __AS3__.vec.Vector;
import flash.display.Bitmap;
import flash.display.BitmapData;
import flash.display.PixelSnapping;
import flash.display.Sprite;
import flash.display.StageAlign;
import flash.display.StageQuality;
import flash.display.StageScaleMode;
import flash.events.Event;
import flash.geom.Matrix3D;
import flash.geom.PerspectiveProjection;
import flash.geom.Rectangle;
import flash.geom.Vector3D;
import net.everyinch.geom.Particle;
[SWF(width="800",height="600",frameRate="32",backgroundColor="0x000000")]
public class ParticleShape1 extends Sprite{
private const MAX_PARTICLES:int = 1024*300;
private var bmpd:BitmapData = new BitmapData(800,600,false,0);
private var buffer:Vector. = new Vector.(800*600,true);
private var focalLength:Number;
private var matrix:Matrix3D = new Matrix3D();
private var particle:Particle;
private var targetX:Number = 0.0;
private var targetY:Number = 0.0;
public function ParticleShape1(){
init();
createParticles();
positionParticles();
addEventListener(Event.ENTER_FRAME,onEnterframe);
}
private function init():void{
stage.align = StageAlign.TOP_LEFT;
stage.scaleMode = StageScaleMode.NO_SCALE;
stage.frameRate = 32;
stage.quality = StageQuality.LOW;
stage.fullScreenSourceRect = new Rectangle(0,0,550,400);
var perspectiveProjection:PerspectiveProjection = new PerspectiveProjection();
perspectiveProjection.fieldOfView = 60;
focalLength = perspectiveProjection.focalLength;
addChild(new Bitmap(bmpd,PixelSnapping.NEVER,false));
}
private function createParticles():void{
if(MAX_PARTICLES < 1) return;
particle = new Particle();
var p:Particle = particle;
var numbers:int = MAX_PARTICLES;
while(--numbers != 0){
p.next = new Particle();
p = p.next;
}
}
// Lorenz Attractors
// 参数:a,b,c,d
// 公式: finalX = x+ad(y-x)
// finalY = y+d(bx-y-zx)
// finalZ = z+d(xy-cz)
private function positionParticles():void{
var a:Number = 16.29;
var b:Number = 11.426;
var c:Number = 4.699;
var dt:Number = 0.058;
var cx:Number = 1;
var cy:Number = 1;
var cz:Number = 1;
var mx:Number = 0;
var my:Number = 0;
var mz:Number = 0;
var scale:Number = 11;
var p:Particle = particle;
while(p != null){
mx = cx + a*dt*(cy-cx);
my = cy + dt*(b*cx-cy-cx*cz);
mz = cz + dt*(cx*cy-c*cz);
cx = mx;
cy = my;
cz = mz;
p.x = mx*scale;
p.y = my*scale;
p.z = mz*scale;
p = p.next;
}
}
private function onEnterframe(e:Event):void{
targetX += (mouseX - targetX)*0.1;
targetY += (mouseY - targetY)*0.1;
matrix.identity();
matrix.appendRotation(targetX,Vector3D.Y_AXIS);
matrix.appendRotation(targetY,Vector3D.X_AXIS);
matrix.appendTranslation(0,0,10);
var p:Particle = particle;
var x:Number;
var y:Number;
var z:Number;
var w:Number;
var pz:Number;
var ix:int;
var iy:int;
var p00:Number = matrix.rawData[0x0];
var p01:Number = matrix.rawData[0x1];
var p02:Number = matrix.rawData[0x2];
var p10:Number = matrix.rawData[0x4];
var p11:Number = matrix.rawData[0x5];
var p12:Number = matrix.rawData[0x6];
var p20:Number = matrix.rawData[0x8];
var p21:Number = matrix.rawData[0x9];
var p22:Number = matrix.rawData[0xa];
var p32:Number = matrix.rawData[0xe];
var width:int = 800;
var min:int = -1;
var max:int = buffer.length;
var i:int;
var b:Vector. = buffer;
var color:uint;
var increment:uint = 0x204444;
var colorMax:uint = 0xFFFFFF;
var cx:Number = 400.0;
var cy:Number = 300.0;
var minZ:Number = 0.0;
var n:int = max;
while(--n > -1){
b[n] = 0x000000;
}
do{
x = p.x;
y = p.y;
z = p.z;
pz = focalLength + x*p02 + y*p12 + z*p22 + p32
if(pz > minZ){
w = focalLength/pz;
ix = int(w*(x*p00+y*p10+z*p20)+cx);
iy = int(w*(x*p01+y*p11+z*p21)+cy);
i = int(ix+int(iy*width));
if(i > min && i < max){ color = b[i]+increment; b[i] = color > colorMax ? colorMax : color;
}
}
p = p.next;
}while(p);
bmpd.lock();
bmpd.setVector(bmpd.rect,b);
bmpd.unlock(bmpd.rect);
}
}
}
转载请注明:陈童的博客 » Flash三维粒子——Lorenz attractor